aurora

外观

DDPM

约 943 字大约 3 分钟

生成模型

2025-04-23

Denoising Diffusion Probabilistic Models

1. Difussion

graph LR
A[x0]-->B[x1]-.-C[xt-1]-->D[xt]-.-E[xT-1]-->F[xT]

扩散过程：

  • 一个固定过程
  • 扩散超参 β

xt−1→xtx_{t-1}\rightarrow x_t：

xt=1−βtxt−1+βtzt,    zt∼N(0,I)x_t= \sqrt{1-\beta_t}x_{t-1}+\sqrt\beta_tz_t,~~~~z_t\sim N(0,I)

β: 10−4∼2−2\beta:~10^{-4}\sim2^{-2}, linear, T≈2000T\approx 2000

令 1−βt=αt1-\beta_t = \alpha_t

xt=αtxt+1−αtzt=αt(αt−1xt−2+1−αt−1zt−1)+1−αtzt\begin{align} x_t &= \sqrt\alpha_tx_t+\sqrt{1-\alpha_t}z_t \notag \\ &= \sqrt\alpha_t(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}z_{t-1})+\sqrt{1-\alpha_t}z_t \notag \\ \end{align}

根据高斯分布的叠加方法：

xt=αtαt−1xt−2+1−αtαt−1z,    z∼N(0,I)x_t=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}z,~~~~z\sim N(0,I) \notag

令 αˉt=∏i=1Tαi\bar\alpha_t = \prod_{i=1}^{T}\alpha_i，得到 x0x_0 与 xtx_t 的关系：

xt=αˉtx0+1−αˉtzx_t = \sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}z

如何取β的值？：αˉ→0,    xT→N(0,I)\bar\alpha\rightarrow0,~~~~x_T\rightarrow N(0,I)

train a model to fit noise in each steps

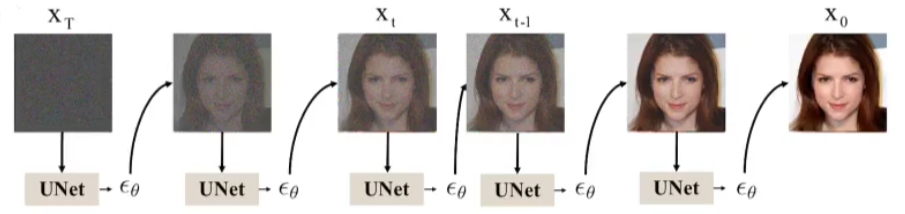
2. Training

假设batch_size = 4，T = 2000

def diffusion_loss_fn(model,x_0,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,n_steps):
    """对任意时刻t进行采样计算loss"""
    batch_size = x_0.shape[0]
    
    #对一个batchsize样本生成随机的时刻t
    t = torch.randint(0,n_steps,size=(batch_size//2,)).to(device)
    t = torch.cat([t,n_steps-1-t],dim=0)
    t = t.unsqueeze(-1)
    
    #x0的系数
    a = alphas_bar_sqrt[t]
    
    #eps的系数
    aml = one_minus_alphas_bar_sqrt[t]
    
    #生成随机噪音eps
    e = torch.randn_like(x_0).to(device)
    
    #构造模型的输入
    x = x_0 * a + e * aml
    
    #送入模型，得到t时刻的随机噪声预测值
    output = model(x,t.squeeze(-1))
    
    #与真实噪声一起计算误差，求平均值
    return (e - output).square().mean()

3. Sampling

根据贝叶斯理论：

q(xt−1∣xt)=q(xt,xt−1)q(xt)=q(xt∣xt−1)q(xt−1)q(xt)q(x_{t-1}|x_t) = \frac{q(x_t,x_{t-1})}{q(x_t)}=\frac{q(x_t|x_{t-1})q(x_{t-1})}{q(x_t)} \notag

目前已知的有：xt−1→xtx_{t-1}\rightarrow x_t，x0→xtx_0 \rightarrow x_t

xt=αtxt−1+1−αtz∼N(αtxt−1,(1−αt)I)⟶q(xt∣xt−1)xt=αˉtx0+1−αˉtz∼N(αˉtx0,(1−αˉt)I)⟶q(xt)\begin{align} x_t &= \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z \sim N(\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)I) \longrightarrow q(x_t|x_{t-1}) \notag \\ x_t &= \sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}z \sim N(\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)I) \longrightarrow q(x_t) \notag \\ \end{align}

q(xt∣xt−1)∼N(αtxt−1,(1−αt)I)q(xt)∼N(αˉtx0,(1−αˉt)I)q(xt−1)∼N(αˉt−1x0,(1−αˉt−1)I)\begin{align} q(x_t|x_{t-1}) &\sim N(\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)I) \notag \\ q(x_t) &\sim N(\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)I) \notag \\ q(x_{t-1}) &\sim N(\sqrt{\bar\alpha_{t-1}}x_0,(1-\bar\alpha_{t-1})I) \notag \end{align}

又因为，高斯分布的密度函数可以写成：N(μ,σ2)∝exp⁡(−12(x−μ)2σ2)N(\mu,\sigma^2)\propto \exp(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2})

q(xt∣xt−1)q(xt−1)q(xt)∝exp⁡[−12((xt−αtxt−1)21−αt+(xt−1−αˉt−1x0)21−αˉt−1−(xt−αˉtx0)21−αˉt)]∝exp⁡{−12[(αtβt+11−αˉt−1)xt−12−2(αtxtβt+αˉt−1x01−αˉt−1)xt−1]+ ...}∝exp⁡[−12(Axt−12+Bxt+C)]∝exp⁡[−12A(xt−1+B2A)2+ ...]\begin{align} \frac{q(x_t|x_{t-1})q(x_{t-1})}{q(x_t)} &\propto\exp[-\frac{1}{2}(\frac{(x_t-\sqrt\alpha_tx_{t-1})^2}{1-\alpha_t}+\frac{(x_{t-1}-\sqrt{\bar\alpha_{t-1}}x_0)^2}{1-\bar\alpha_{t-1}}-\frac{(x_t-\sqrt{\bar\alpha_t}x_0)^2}{1-\bar\alpha_t})] \notag \\ & \propto \exp\{-\frac{1}{2}[(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}})x_{t-1}^2-2(\frac{\sqrt\alpha_tx_t}{\beta_t}+\frac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}})x_{t-1}]+~ ... \} \notag\\ & \propto \exp[-\frac{1}{2}(Ax^2_{t-1}+Bx_t+C)]\notag\\ & \propto \exp[-\frac{1}{2}A(x_{t-1}+\frac{B}{2A})^2+~...] \notag \end{align}

提取系数，A=αtβt+11−αˉt−1A = \frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}，B=−2(αtxtβt+αˉt−1x01−αˉt−1)B=-2(\frac{\sqrt\alpha_tx_t}{\beta_t}+\frac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}})

所以，μ=B2A\mu = \frac{B}{2A}，σ2=1A\sigma^2=\frac{1}{A}

σ2=1A=1αtβt+11−αˉt−1=βt(1−αˉt−1)1−αtαˉt−1=1−αˉt−11−αˉtβt\begin{align} \sigma^2 &=\frac{1}{A} \notag \\ &=\frac{1}{\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}} \notag \\ &=\frac{\beta_t(1-\bar\alpha_{t-1})}{1-\alpha_t\bar\alpha_{t-1}} \notag\\ &=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \end{align}

μ=B2A=(αtxtβt+αˉt−1x01−αˉt−1)1−αˉt−11−αˉtβt=αtxt(1−αˉt−1)1−αˉt+αˉt−1x0βt1−αˉt=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉtx0\begin{align} \mu &= \frac{B}{2A} \notag \\ &=(\frac{\sqrt\alpha_tx_t}{\beta_t}+\frac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}})\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \notag \\ & =\frac{\sqrt{\alpha_t}x_t(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}+\frac{\sqrt{\bar\alpha_{t-1}}x_0\beta_t}{1-\bar\alpha_t} \notag \\ &= \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}x_0 \end{align}

因为 xt=αtxt−1+1−αtzx_t = \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z ，x0=1αˉt(xt−1−αˉtz~)x_0 = \frac{1}{\sqrt{\bar\alpha_t}}(x_t-\sqrt{1-\bar\alpha_t}\tilde z )，带入 μ\mu

μ=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉt1αˉt(xt−1−αˉtz~)=xtαˉt(αt−αˉt+βt1−αˉt)+z~αtβt1−αˉt=1αt(xt−βt1−αˉtz~)\begin{align} \mu&=\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}\frac{1}{\sqrt{\bar\alpha_t}}(x_t-\sqrt{1-\bar\alpha_t}\tilde z) \notag \\ & =\frac{x_t}{\sqrt{\bar\alpha_t}}(\frac{\alpha_t-\bar\alpha_t+\beta_t}{1-\bar\alpha_t})+\frac{\tilde z}{\sqrt{\alpha_t}}\frac{\beta_t}{\sqrt{1-\bar\alpha_t}} \notag \\ & = \frac{1}{\sqrt\alpha_t}(x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\tilde z) \end{align}

wenwei@2025