aurora

外观

SR3

约 2038 字大约 7 分钟

2024-08-11

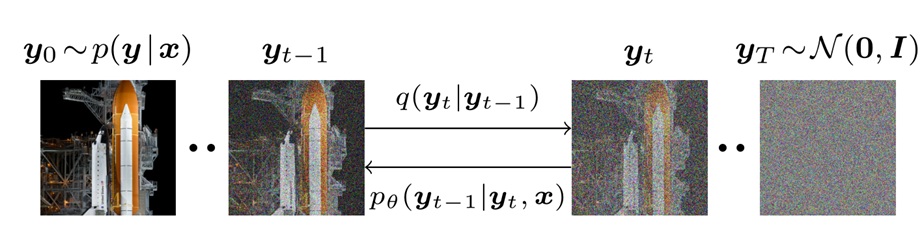
SR3 的工作原理是通过一系列细化步骤学习将标准正态分布转换为经验数据分布。灵感来自最近关于去噪扩散概率模型 (DDPM) 和去噪分数匹配 的工作。

将超分任务描述成一个有条件生成

  • 将 LR 作为条件，与噪声图 concat 后送入Unet
  • 不再直接取 αˉt\bar\alpha_t，而是取均匀分布 [αˉt−1,αˉt][\bar\alpha_{t-1},\bar\alpha_t]
  • 不再输入t给unet，而是直接输入 noise level，也就是上一条中均匀采样的值

xt=αˉtx0+1−αˉtzx_t = \sqrt{\bar\alpha_t}x_0 + \sqrt{1-\bar\alpha_t}z

z~=Unet(xt,t)\tilde{z}=Unet(x_t,t)

z~=Unet(xt,αˉt)\tilde{z}= Unet(x_t,\bar\alpha_t)

通过噪声level，跳步生成过程

(NIPSW 22')Palette: Image-to-Image Diffusion Models

Palette: Image-to-Image Diffusion Models (iterative-refinement.github.io)

对 unet ，损失函数添加条件项，未开源

生成模型

假定我们有一个数据集 {x1,x2,…,xN}\left \{ x1, x2, … , xN \right \} 其中的每个 xixi 都是从一个潜在的数据分布 pθ(x)p_θ (x) 中独立取得的

生成模型的目的是能够完美的建模这个数据分$p_θ (x) $,以便任意的采样都能生成符合这个分布的新数据。

  • 设定，fθ(x)∈Rf_θ ( x ) ∈ R是一个以θ 为参数的函数

  • 为了构造这个模型需要一种表示这种概率分布的方式

概率密度函数

pθ(x)=e−fθ(x)zθ{\Large p_\theta (x)=\frac{e^{-f_\theta(x)}}{z_\theta }}

ZθZ_θ：归一化常数，使得概率密度函数积分为一

fθ(x)f_θ (x) ：非归一化的概率模型

  • 对于任意一般情况下的fθ(x)f_θ (x)，归一化常数非常难求

score-based models

通过构造一个score function而非density function来避开处理这个规则化常数的问题。

对一个分布P(x) ， 其score function定义为:（Stein score function）

∇xlog⁡p(x)∇_x log⁡p(x)

使用这种score function的模型我们就统称为score-based model，用 sθ(x)s_θ (x)表示

sθ(x)=∇xlog pθ(x)=−∇xfθ(x)+∇xlog Zθ⏟=0=−∇xfθ(x){\Large s_\theta (x)=\nabla _xlog~p_\theta(x)=-\nabla _xf_\theta (x)+\underset{=0}{\underbrace{\nabla _xlog~Z_\theta }}=-\nabla _xf_\theta (x)}

  • 排除掉 ZθZ_θ，无需通过设计复杂的结构处理

Estimation of Non-Normalized Statistical Models by Score Matching

  • Score Matching 的抽象逻辑其实可以用一句话概括：通过最小化模型的对数密度梯度（gradient of the log-density）和 观测数据的对数密度梯度 的期望平方距离 来估计参数。

    ​

    Ep(x)[∣∣∇xlog p(x)−sθ(x)∣∣22]\mathbb{E}_{p(x)}[||\nabla _xlog~p(x)-s_\theta (x)||_{2}^{2} ]

    • 可以在给定数据上通过梯度下降的方式估计得到
    • 如果处理不了形式复杂的函数，那就处理这个函数的导数
    • sθ(x)s_θ (x)代表梯度预测网络。

∇θEpdata[∣∣sθ(x)−∇xlog⁡pdata(x)∣∣22]=∇θEpdata [∣∣sθ(x)∣∣22+(∇xlog⁡pdata(x))(∇xlog⁡pdata(x))T]−2sθ(x)(˙∇xlog⁡pdata(x))T=∇θEdata[∣∣sθ(x)∣∣22]+0−2∇θEpdata [sθ(x)⋅∇xpdata(x)pdata(x)]=∇θEdata[∣∣sθ(x)∣∣22]−2∇θ∫sθ(x)⋅∇xpdata(x)dx(∫∇x(sθ(x)⋅∇xpdata(x))dx=sθ(x)⋅pdata(x)∣x→−∞x→+∞≡0=∇θEdata[∣∣sθ(x)∣∣22−2tr(∇xsθ(x))](Our  Training Object)\large \begin{equation} \begin{split} \nabla _\theta &E_{p_{data}}[||s_\theta (x)-\nabla _x\log p_{data}(x)||_2^2]\\ &=\nabla _\theta E_{p_{data}~}[||s_\theta (x)||_2^2+(\nabla _x\log p_{data}(x))(\nabla _x\log p_{data}(x))^T]-2s_\theta (x)\dot(\nabla _x\log p_{data}(x))^T\\ &=\nabla _\theta E_{data}[||s_\theta (x)||_2^2]+0-2\nabla _\theta E_{p_{data}~}[s_\theta(x) ·\frac{\nabla _xp_{data}(x)}{p_{data}(x)} ]\\ &=\nabla _\theta E_{data}[||s_\theta (x)||_2^2]-2\nabla _\theta \int s_\theta (x)·\nabla _xp_{data}(x)dx\\ &(\int \nabla _x(s_\theta (x)·\nabla _xp_{data}(x))dx=s_\theta(x)·p_{data}(x)|_{x\to -\infty }^{x\to +\infty }\equiv 0\\ &=\nabla _\theta E_{data}[||s_\theta (x)||_2^2-2tr(\nabla _xs_\theta(x))]\\ &\text{(Our ~Training~Object)} \end{split} \end{equation}

变换后的公式不需要显式的概率密度pθ(x)p_θ (x)，因此可求，但是含有梯度计算，计算量巨大

  • 目标函数 E qσ(x^∣x)pdata(x)[∣∣sθ(x^)−∇x^ log⁡qσ(x^∣x)∣∣22]E_{~{q_\sigma}(\hat{x}|x)p_{data}(x)}[||s_\theta(\hat{x})-\nabla_{\hat{x}~}\log q_\sigma(\hat{x}|x)||_2^2]

    • 真实带噪数据
    • 模型扩散过程中（扰动后）的对数密度梯度

  • 噪声为高斯噪声时 ，可化简。

  • 用一种特定的噪声分布来扰动原始数据，用score matching的方法去估计扰动后的数据分布的score。

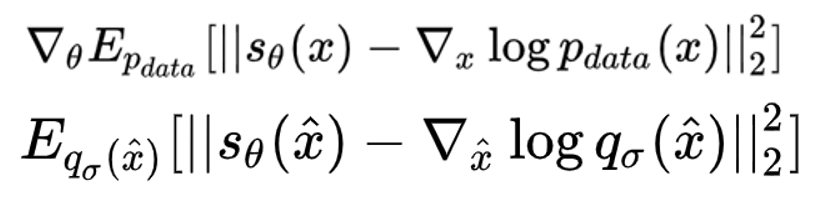
  • 当噪声十分小的时候，有近似：qσ(x)≈pdata(x)q_\sigma(x)\approx p_{data}(x) image-20220811220638055

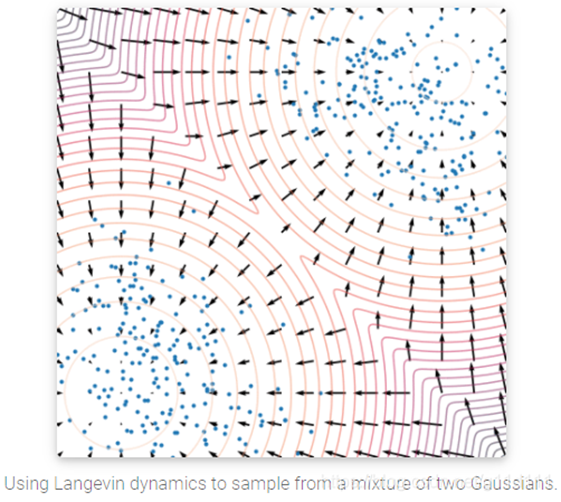
Langevin dynamics

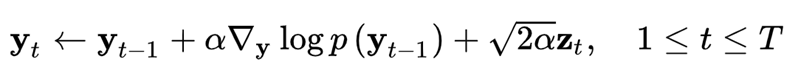
image-20220811220310791

  • 仅通过使用score function $∇_x log⁡p(x) $来对真实数据分布P(x)进行MCMC采样

  • MCMC, 马尔科夫链蒙特卡洛(Markov Chain Monte Carlo)方法,是用于从复杂分布中获取随机样本的统计学算法

  • $z_t\sim\mathcal{N}(0,I) $，α 是步长

https://ieeexplore.ieee.org/abstract/document/6795935

DDPM

image-20220811220237345

让模型输出和随机生成的噪音 距离差值最小。我们的模型的目标其实就是在生成噪音。

α 为超参

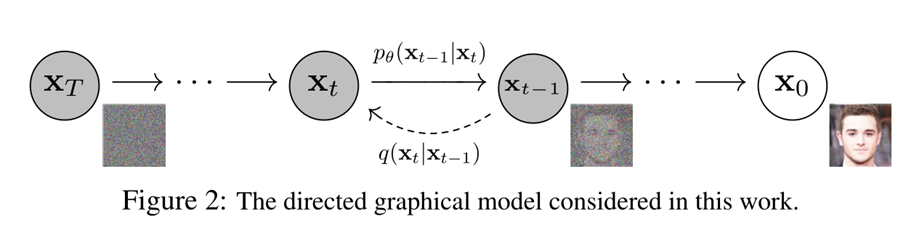
扩散过程就是从初始状态也是观测值（x0）开始，一步步添加高斯噪音，直到步数T足够多之后，噪音将原始输入信号完全淹没，得到一个纯的高斯噪声（xT）。

每一步得到的图片都可以看成是初始值和标准高斯噪音的一个线性组合，如果可以预测到，就可以在反向过程将每一步t中的噪声信息从x中抽取出来，起到去噪的效果。

生成真实信号与标准高斯分布噪音之间多余的那部分噪音信号，我们可以通过用 标准高斯分布噪音 减去 生成的噪音信号 得到我们最后的 合成信号。

SR3

image-20220617193939032

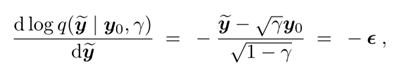
  • 前向马尔可夫扩散过程 q，它在 T 次迭代中逐渐将高斯噪声添加到高分辨率图像 y0 中。

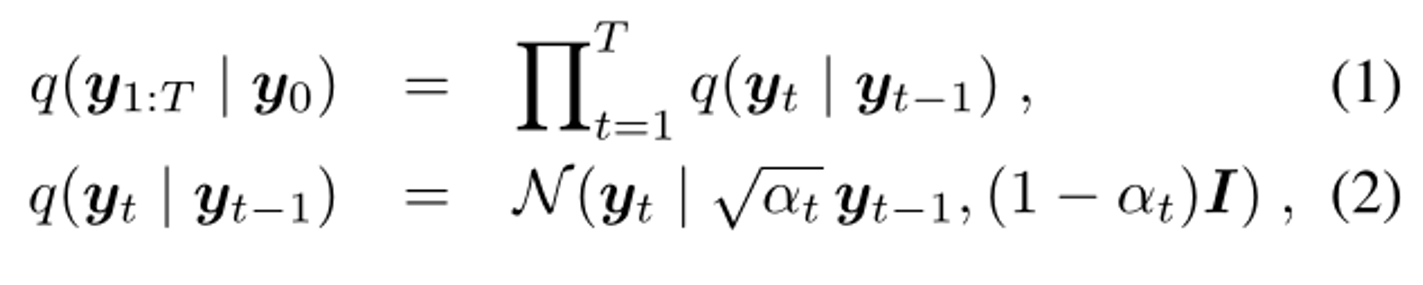
  • 扩散的过程是人为拟定好的过程，主要训练的是反向的去噪过程。

  • 模型fθ(x,y^,γ)f_\theta(x,\hat{y},\gamma)将噪声的方差 γγ 的充分统计量作为输入，并被训练用来预测噪声向量 εε。通过调节标量 γγ，使模型了解噪声水平。

训练过程

训练集为图像对（LR，HR）

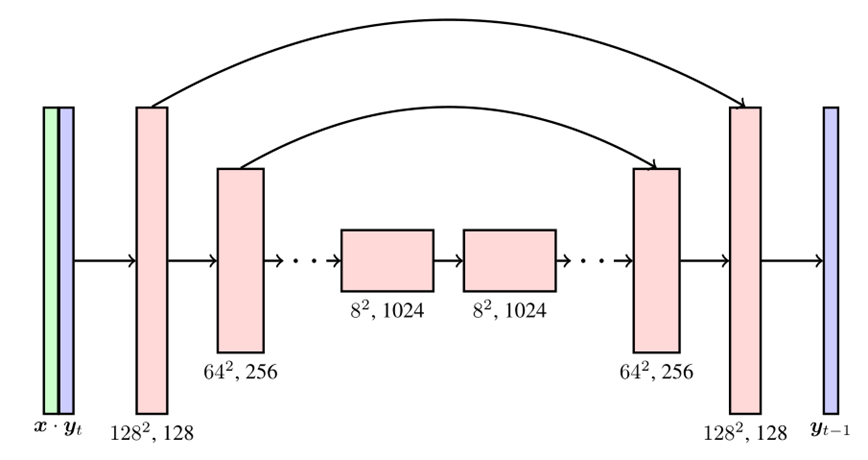
模型输入包括：

  • LR图像x。
  • 含噪图像 yt ，其中 y0 为HR图像，由下面公式得到：
image-20220811220839545

α为超参,γ与训练次数t相关

使得模型输出的噪声与随机采样的高斯噪声差距尽可能小。

推理过程

输入为低分辨率图像x以及高斯噪声yt，输出为高分辨率图像。 输入通过公式重复迭代T次得到SR图像

类似于 Langevin 动力学的一个步骤，其中f_θ 提供了数据对数密度梯度的估计

实验结果

人脸图像：训练集为FFHQ，评估集为CelebA-HQ

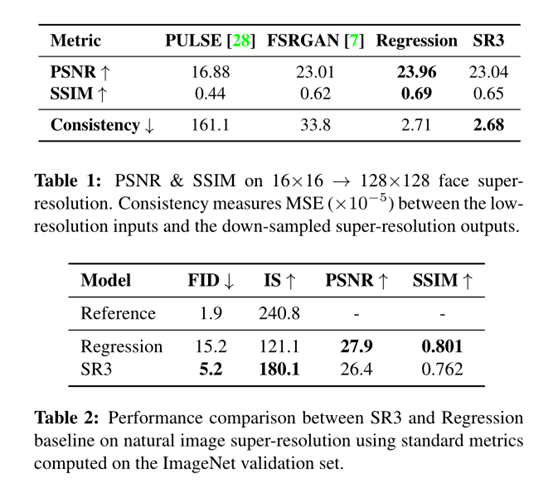
表 1 显示了 16×16 → 128×128 人脸超分辨率的 PSNR、SSIM [59] 和 Consistency 分数。SR3 在 PSNR 和 SSIM 上的表现优于 PULSE 和 FSRGAN，而在回归基准上的表现稍差。当输入分辨率低且放大因子大时，这些传统的自动评估措施与人类感知的相关性不佳。

PSNR和SSIM等自动图像质量分数通常会惩罚合成的高频细节，例如头发纹理，因为合成细节和参考细节并不完全一致，所以与基于 MSE 回归的技术相比差一些。

自然图像：训练集与评估集为ImageNet

SR3 的输出实现了更高的样本质量分数（FID 和 IS），但 PSNR 和 SSIM 比回归差。

Generative Modeling by Estimating Gradients of the Data Distribution | Yang Song (yang-song.net)

SR3: Iterative Image Enhancement (iterative-refinement.github.io)

另辟蹊径—Denoising Diffusion Probabilistic 一种从噪音中剥离出图像/音频的模型 - 知乎 (zhihu.com)

生成模型新方向

SR3:Image Super-Resolution via Iterative Refinement - 知乎 (zhihu.com)

Denoising Diffusion Probabilistic Models (DDPM) - 馒头and花卷 - 博客园 (cnblogs.com)

wenwei@2025