aurora

外观

Score based Diffusion model

约 669 字大约 2 分钟

扩散模型

[ 生成模型新方向]: score-based generative models_sooner高的博客-CSDN博客

Generative Modeling by Estimating Gradients of the Data Distribution | Yang Song (yang-song.net)

生成模型分类：

  1. likelihood based models
    • 直接队数据分布进行你和
      • VAE
      • normalizing flow models
    • 缺点：对于网络结构设计有很大限制
  2. implicit generative models
    • 间接对数据分布进行拟合
      • GANs
    • 缺点：往往需要对抗学习，不容易训练

方法

score based model 不是直接学习概率分布，而是学习 score.

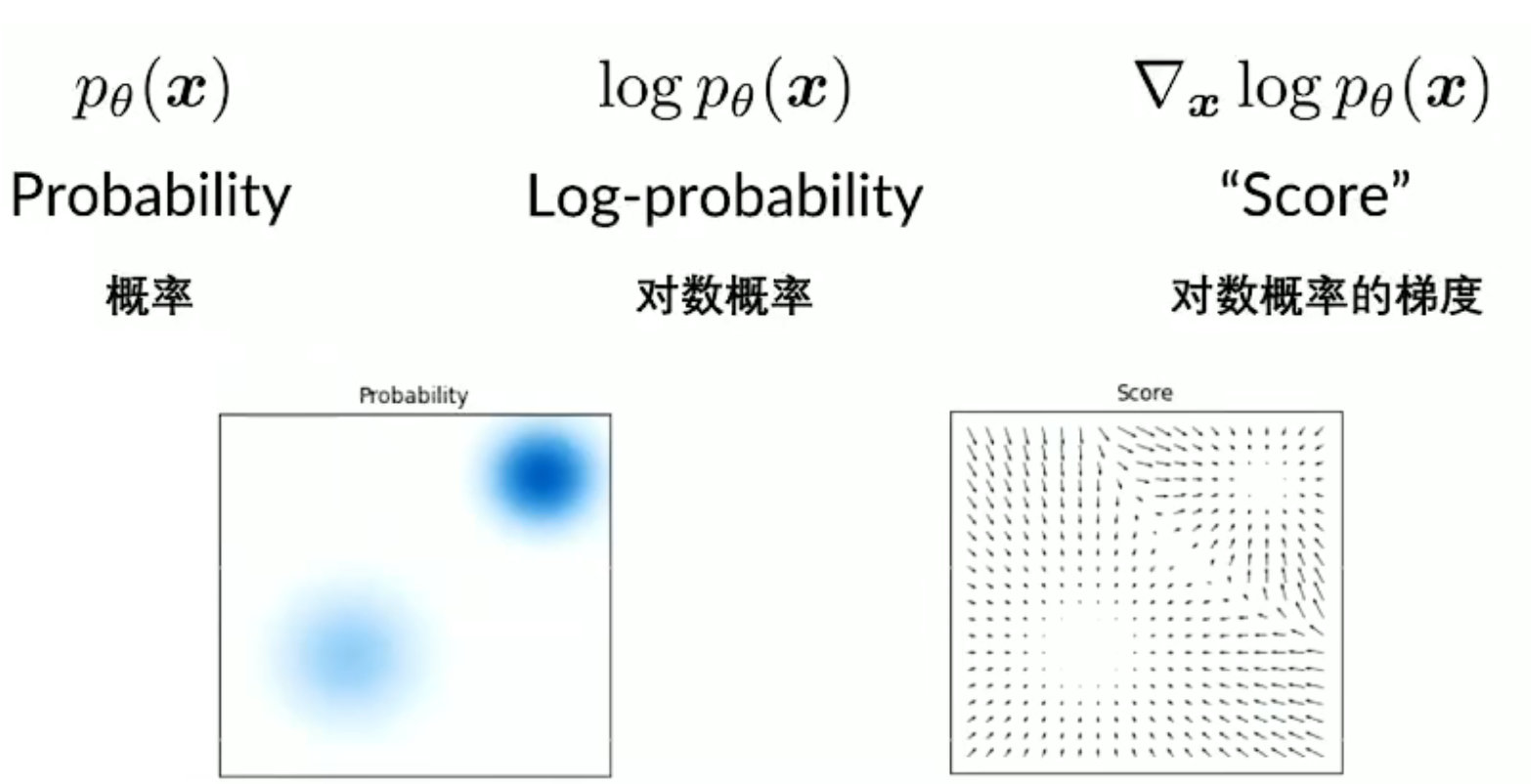
  • 假设我们通过某种方法（score match）得到了 score 模型：sθ(x)≈∇xlog⁡p(x)s_{\theta}(x)\approx \nabla_x\log p(x)

  • 通过郎之万动力学的迭代过程从任意一个分布走到目标分布：

    xi+1←xi+ϵ∇xlog⁡p(x)+2ϵzi,    i=0,1,...,k,x_{i+1}\gets x_i +\epsilon\nabla_x\log p(x)+\sqrt{2\epsilon}z_i,~~~~i=0,1,...,k,

  • 上式给出了一种从随机采样噪声出发一步步逼近目标数据的方法

    • ϵ\epsilon 步长

问题

在数据密度较低的位置，score的估计往往是不准确的

  • 导致在推理的早期，模型容易根据错误的梯度二脱轨

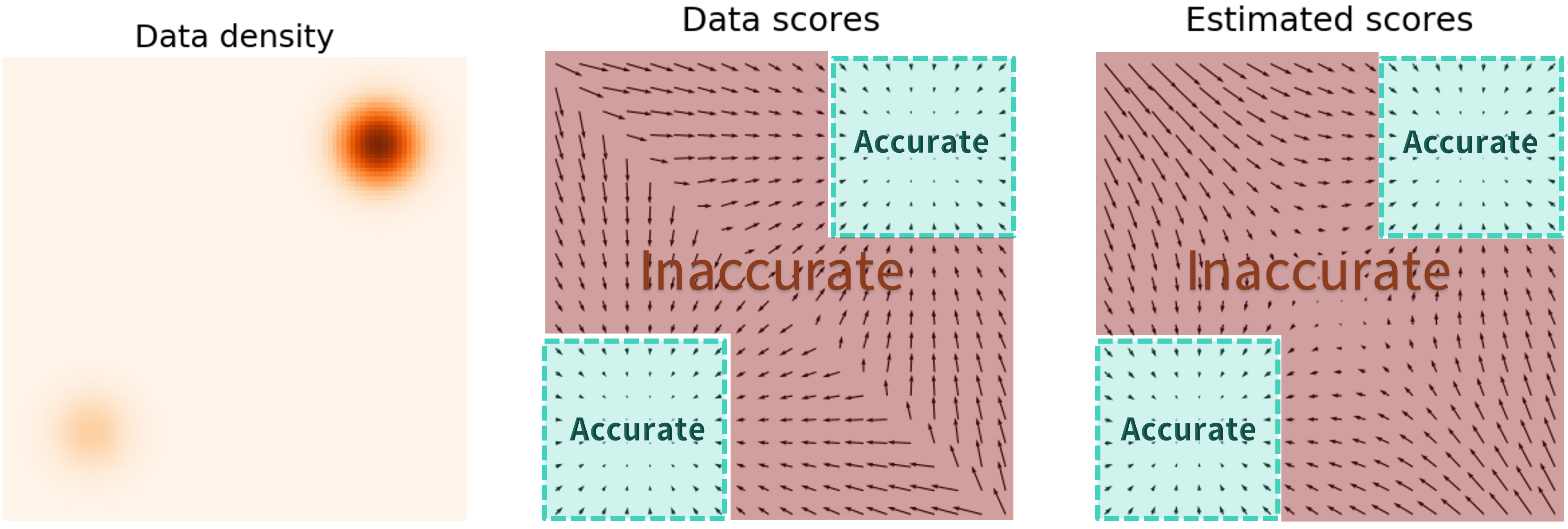
    Estimated scores are only accurate in high density regions.

  • 解决方法

对数据加噪声，扩大数据范围，增加可以准确估计score的区域

2

要加少强度的噪声？

  • 较弱的噪声——避免损害原本的数据分布——无法在大多数区域准确估计score

  • 较强的噪声——损害原本的数据分布——更多区域可以准确估计score

  • 解决方法：

    • 在推理的不同阶段加不同强度的噪声，从大到小

求 score

DDPM的噪声假设：xt∼N(αtˉx0,(1−αtˉ)I)x_t \sim N(\sqrt{\bar{\alpha_t}}x_0,(1-\bar{\alpha_t})I)

密度分布函数：p(xt)∝exp⁡{−(xt−αtˉx0)⊤(xt−αtˉx0)2(1−αˉt)}p(x_t)\propto\exp\{-\frac{(x_t-\sqrt{\bar{\alpha_t}}x_0)^\top (x_t-\sqrt{\bar{\alpha_t}}x_0)}{2(1-\bar\alpha_t)}\}

score: ∇xtlog⁡p(xt)\nabla_{x_t}\log p(x_t)

推导：∇xtlog⁡p(xt)=−xt−αtˉx01−αˉt\nabla_{x_t}\log p(x_t)=-\frac{x_t-\sqrt{\bar{\alpha_t}}x_0}{1-\bar\alpha_t}

score 和加在原图上的噪声仅仅相差一个系数的关系，可以用一个噪声估计网络来估计

目标函数：

∑i=1Lλ(i)Epσi(x)[∥∇xlog⁡pσi(x)−sθ(x,i)∥22],\begin{equation} \sum_{i=1}^L \lambda(i) \mathbb{E}_{p_{\sigma_i}(\mathbf{x})}[\| \nabla_\mathbf{x} \log p_{\sigma_i}(\mathbf{x}) - \mathbf{s}_\theta(\mathbf{x}, i) \|_2^2], \end{equation}

  • 不同噪声尺度的加权结果

image inpainting

pic

1

总结

为什么要加噪声：

增加扰动，扩大数据范围，增加可以准确估计score的区域

为什么要估计噪声：

估计噪声就是估计score，也就是估计数据分布的对数梯度

wenwei@2025