Deep Marching Tetrahedra: a Hybrid Representation for High-Resolution 3D Shape Synthesis (nv-tlabs.github.io)

深度3D条件生成模型

使用简单的用户指导生成精细的3d形状

结合隐式和显式3d呈现方法

• 与训练有符号距离值回归的当前隐式方法相比，DMTET 直接优化重建表面，这使我们能够以更少的伪影合成更精细的几何细节。
• 与直接生成网格等显式表示的深度 3D 生成模型不同，我们的模型可以合成具有任意拓扑结构的形状。

核心构成：

• 可形变的四面体网格：
  • 顶点由 SDF 编码
• 可微的 marching tetrahedra layer ：
  • 将隐式的 SDF 编码转换成显式的mesh

3D Representation

​

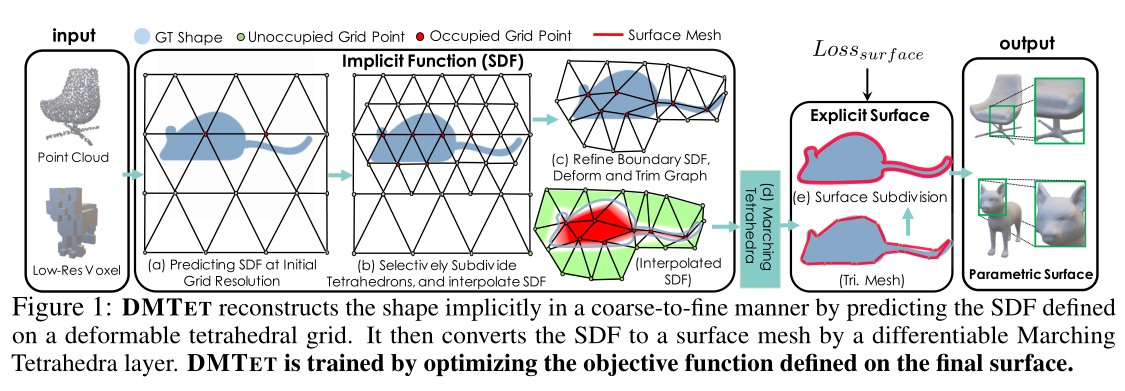
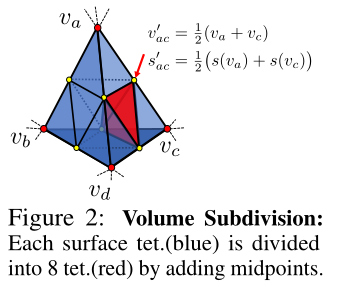
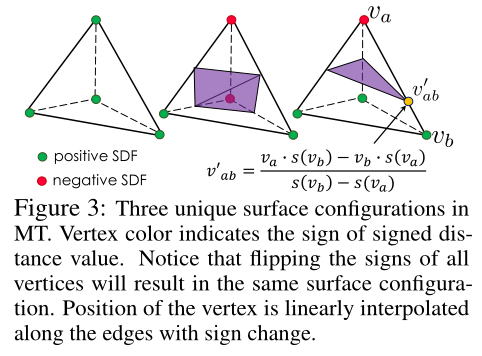
SDF：符号距离场

Model

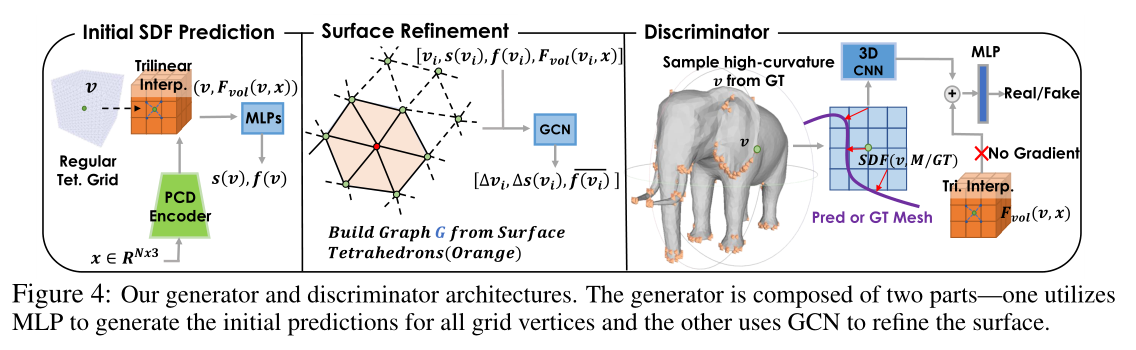
Input encoder

使用PVCNN作为输入编码器，从点云中提取一个三维特征体$F_{vol}(x)$。当输入是一个粗体素形状时，我们对其表面的点进行采样。我们通过三线插值为一个网格顶点$v∈\R^3$计算一个特征向量$F_{vol}(v, x)$。

Initial Prediction of SDF

• 使用一个全连接的网络$s(v)=MLP(F_{vol}(v, x), v)$来预测初始可变形四面体网格中每个顶点的SDF值。

• 全连接网络另外输出一个特征向量$f(v)$，用于体积细分阶段的表面细化。

Surface Refinement with Volume Subdivision

1. 在获得初始SDF后，迭代细化表面，并对四面体网格进行细分。
   • 首先根据当前的$s(v)$值来识别表面四面体$T_{surf}$。
   • 然后我们建立一个图 $G = (V_{surf} , E_{surf} )$，其中$V_{surf} , E_{surf}$对应于$T_{surf}$的顶点和边。
   • 然后使用图形卷积网络（GCN）预测$V_{surf}$中每个顶点 $i$ 的位置偏移量 $\Delta vi$ 和 SDF 残差值 $\Delta s(vi)$

$$\begin{align} f^{'}_{v_i} &=concat(v_i,s(v_i),F_{vol}(v_i,x),f(v_i)) \\ (\Delta v_i,\Delta s(v_i),\overline{f(v_i)})_{i=1,...N_{surf}} &=GCN((f^{'}_{v_i})_{i=1,...N_{surf}},G) \end{align}$$

其中 $N_{surf}$ 是 $V_{surf}$ 中顶点的总数，$f(vi)$ 是更新的每个顶点特征。

顶点位置 $v_i $和顶点 的SDF值被更新为 $v^{'}_i = v_i +\Delta v_i$，$s(v^{'}_i) = s(v_i) + \Delta s(v_i)$。

这个细化步骤有可能翻转SDF值的符号以细化局部类型学，也可以移动顶点从而改善局部几何。

2. 在表面 refinement 之后，我们进行体积细分步骤，然后再进行额外的表面细化步骤。

   • 特别是，我们重新识别 $T_{surf}$ 并对 $T_{surf}$ 和它们的近邻进行细分。

   • 在这两个步骤中，我们将未细分的四面体从完整的四面体网格中删除，这样可以节省内存和计算量

     因为$T_{surf}$ 的大小与物体的表面积成正比，并且随着网格分辨率的提高，其大小呈四次方而非三次方扩展。

请注意，顶点的SDF值和位置是继承自细分前的层次，因此，在最终表面计算的损失可以反向传播到所有层次的所有顶点。因此，我们的DMTET自动学习细分四面体，不需要像先前的工作那样在中间步骤中增加损失项来监督八叉树层次结构的学习。

Learnable Surface Subdivision

在使用MT提取表面网格后，我们可以进一步应用可学习的表面细分。具体来说，我们在提取的网格上建立一个新的图形，并使用GCN来预测每个顶点 $v^{'}_i$ 的更新位置，以及用于Loop Subvidision的 $α_i$。这一步消除了量化误差，并通过调整 $α_i$ 减轻了经典环形细分法的近似误差，这些误差在经典方法中是固定的。??

3D discriminator

我们在从生成器预测的最终表面上应用一个三维判别器 $D$。我们根据经验发现，使用DECOR-GAN中的一个三维CNN作为从预测的网格中计算出来的有符号距离场的判别器，可以有效地捕捉局部细节。

具体来说，我们首先从目标网格中随机选择一个高曲率的顶点 $v$，并在 $v$ 周围的体素化区域计算出 ground truth 的符号距离场 $S_{real}∈\R^{N×N×N}$。同样，我们在同一位置计算出预测表面网格 $M$ 的符号距离场，得到 $S_{pred}∈\R^{N×N×N}$。

注意，$S_{pred}$是网格 $M$ 的解析函数，因此 $S_{pred}$ 的梯度可以反向传播到M中的顶点位置。我们将$S_{real}$或$S_{pred}$与位置 $v$ 的特征向量 $F_{vol}(v, x)$一起输入判别器。判别器然后预测指示输入是来自真实形状还是生成形状的概率。

损失函数

表面对齐损失

对抗损失

正则化损失