摘要

3D 语义占用预测是自动驾驶中一项重要的任务，它能够预测周围场景的精细几何形状和语义信息。大多数现有方法采用基于密集网格的场景表示，忽略了驾驶场景的空间稀疏性。尽管 3D 语义高斯（Gaussian）作为一种以目标为中心的稀疏替代方案，但大多数高斯仍然以低效的方式描述空区域。为了应对这一问题，我们提出了一个概率高斯叠加模型，该模型将每个高斯解释为其邻域被占用的概率分布，并通过概率乘法来推导整体几何形状。此外，我们采用精确的高斯混合模型进行语义计算，以避免高斯之间的不必要重叠。为了在非空区域有效初始化高斯，我们设计了一个基于分布的初始化模块，该模块学习像素对齐的占用分布，而不是表面的深度。我们在 nuScenes 和 KITTI-360 数据集上进行了广泛的实验，结果表明，我们的 GaussianFormer-2 在效率极高的情况下实现了最先进的性能。代码地址：github。

1. 引言

在自动驾驶中，以视觉为中心的系统相比基于激光雷达（LiDAR）的系统更具成本效益。然而，它们无法捕捉任意形状的障碍物，这对驾驶的安全性和可靠性构成了挑战。3D 语义占用预测方法的出现缓解了这一限制，通过预测周围 3D 环境的精细几何形状和语义信息，支持了一系列新兴应用，包括端到端自动驾驶、4D 占用预测以及自监督 3D 场景理解。

尽管应用前景广阔，但 3D 语义占用预测本质上是一个密集的三维分割任务，需要对 3D 场景进行既高效又有效的表示。

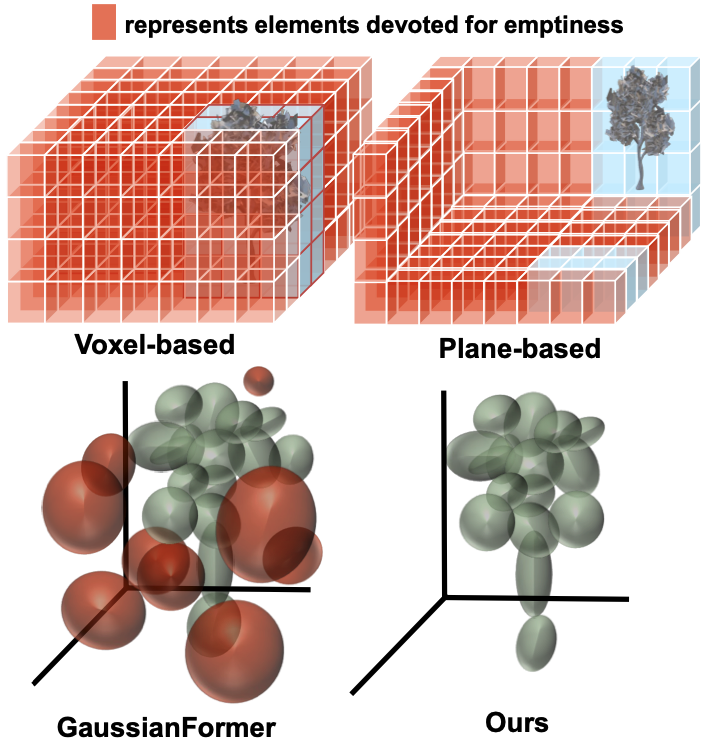
• 基于体素的方法使用密集的 3D 体素作为表示来描述场景的最细细节，但它们忽略了 3D 占用的空间冗余性，导致计算复杂性高。作为一种解决方案，平面表示（如 BEV 和 TPV）沿一个轴压缩 3D 网格以得出 2D 特征图，从而减少令牌数量。然而，它们在建模环境时仍然会考虑空区域，这削弱了它们的模型容量和效率。

• 作为以目标为中心的稀疏场景表示的先驱，3D 语义高斯通过为每个高斯学习均值、协方差、不透明度和语义来以稀疏的方式描述 3D 空间。然而，当前的 3D 语义高斯表示仍存在一些限制：首先，每个高斯仍然可以描述空区域，在 3D 占用的空间稀疏性下，这使得大多数高斯在以目标为中心的公式中变得无用；其次，聚合过程忽略了重叠问题，直接将每个高斯的贡献相加以产生占用预测，这导致语义对数无界，并进一步增加了高斯之间的重叠。因此，独立描述占用区域的有效高斯的比例可能极低，这削弱了 3D 语义高斯表示的效率。

在本文中，我们引入了一个概率高斯叠加模型，以解决 3D 语义高斯的上述限制并提高其利用效率。

提示

具体来说，我们提出了概率高斯表示，将 3D 高斯分配为仅对非空区域进行建模，通过将每个高斯解释为其邻域被占用的概率分布。我们采用概率的乘法定理来聚合独立的概率分布，并推导出几何预测。

此外，我们将高斯混合模型整合到我们的概率高斯表示中，以生成归一化的语义预测，从而避免无界对数并防止高斯之间不必要的重叠。由于我们的表示仅对占用区域进行建模，我们还设计了一个基于分布的初始化模块，以有效地在非空区域周围初始化高斯，该模块学习像素对齐的占用分布，而不是表面的深度值。我们在 nuScenes 和 KITTI-360 数据集上进行了广泛的实验，分别用于环绕视图和单目 3D 语义占用预测。我们的 GaussianFormer-2 以高效率实现了最先进的性能。此外，定性的可视化结果表明，GaussianFormer-2 能够生成既整体又逼真的场景感知。

2. 相关工作

3D 语义占用预测已成为自动驾驶中一种有前景的环境建模方法，因为它以全面的方式描述驾驶场景。该任务的目标是根据一种或多种传感器的输入，对场景中的每个体素进行标记。最常用的两种传感器是激光雷达和相机。尽管基于激光雷达的方法在 3D 感知任务中表现非常出色，但它们在恶劣天气条件下以及检测远距离物体方面存在局限性；因此，基于相机的方法越来越受到关注。早期的 3D 语义占用预测工作采用密集网格表示作为直接方法来得出占用情况，随后的工作转向稀疏以目标为中心的表示，以解决密集表示固有的冗余问题。

基于网格的场景表示：平面表示已成为自动驾驶场景感知任务中的有力竞争者。

• BEVFormer 是该领域的开创性工作，它仅使用相机输入，在检测和分割任务中表现与基于激光雷达的方法相当。它将图像特征转换为鸟瞰图（BEV）特征作为统一的场景表示，因为从这个视角来看，信息最为多样化。然后将 BEV 特征用于下游任务。然而，BEV 特征不适合用于 3D 占用构建，因为它会导致高度信息丢失。
• 作为 BEV 空间的推广，TPVFormer 提出了三视角表示，以包含高度信息，从而使其更适合 3D 场景。另一个研究方向采用基于体素的表示，作为一种更具 3D 特性和细粒度的方法，使其成为 3D 体积语义预测的热门选择。

然而，这些方法使用密集网格表示，无论环境的空间稀疏性如何，都平等地描述每个体素，从而导致固有的冗余。

以目标为中心的场景表示：为了消除密集表示固有的空间冗余性，许多近期工作采用稀疏表示。

• 一种方法将密集网格划分为物体出现的区域，并省略被视为为空的区域。然而，非空区域可能会被错误地归类为未占用区域，并从整个后续过程中完全消除。
• 另一种方法利用点表示，通过在场景范围内采样点作为后续细化过程中的查询点。然而，点的描述范围有限，因为它没有空间范围。
• 另一种方法是 GaussianFormer，它采用 3D 语义高斯表示，概率围绕均值分布，允许更多的利用。然而，由于没有规定高斯不能代表空区域，空间冗余仍然存在。

3. 提出的方法

在本节中，我们介绍了用于高效 3D 语义占用预测的概率高斯叠加方法。我们首先回顾原始的 3D 语义高斯表示及其限制（第 3.1 节）。然后，我们介绍我们的概率高斯建模以及我们如何根据概率的乘法定理和高斯混合模型推导出几何和语义预测（第 3.2 节）。最后，我们详细介绍了基于分布的初始化模块，以有效地在占用区域周围初始化概率高斯（第 3.3 节）。

3.1 3D 语义高斯表示

以视觉为中心的 3D 语义占用预测旨在获得 3D 场景的精细几何形状和语义信息。具体来说，目标是根据输入图像 $I = \{I_i\}_{i=1}^N$预测体素级语义分割结果 $O \in \mathbb{C}^{X \times Y \times Z}$，其中 $C$、$\{X, Y, Z\}$和 $N$分别表示预定义的类别集合、占用的空间分辨率和输入视图的数量。

为了实现这一目标，3D 语义高斯表示采用一组 $P$个高斯基元 $G = \{G_i\}_{i=1}^P$，每个 $G_i$使用其均值 $m_i$、尺度 $s_i$、旋转 $r_i$、不透明度 $a_i$和语义 $c_i$来描述一个局部区域。GaussianFormer 将这些基元解释为局部语义高斯分布，通过加性聚合对整体占用预测做出贡献：

$$\hat{o}(x; G) = \sum_{i=1}^{P} g_i(x; m_i, s_i, r_i, a_i, c_i),$$

其中

• $g_i(x; \cdot)$表示第 $i$个语义高斯对 $\hat{o}(x; G)$的贡献，
• $\hat{o}(x; G)$是位置 $x$处的整体占用预测。

贡献 $g$进一步计算为位置 $x$处对应的语义高斯分布：

$$g(x; G) = a \cdot \exp\left(-\frac{1}{2}(x - m)^T \Sigma^{-1}(x - m)\right) c,$$

$$\Sigma = R S S^T R^T, \quad S = \text{diag}(s), \quad R = q2r(r),$$

其中 $\Sigma$、$R$和 $S$分别表示协方差矩阵、由四元数 $r$构造的旋转矩阵（使用函数 $q2r(\cdot)$）以及从函数 $\text{diag}(\cdot)$得到的对角尺度矩阵。

尽管由于高斯分布的可变形性，与密集体素的数量相比，高斯的数量有所减少，但 3D 语义高斯表示仍存在一些限制。

• 首先，它以相同的方式使用语义属性 $c$来描述占用和未占用区域，导致在户外场景中由于空旷空间的巨大比例，大多数高斯被归类为空。
• 其次，语义高斯表示鼓励高斯之间重叠，因为聚合过程独立地将每个高斯的贡献相加，导致无界占用预测 $\hat{o}$。为了优化，模型会学习分配更多高斯来描述同一区域，由于 $\hat{o}$的无界性，这加剧了高斯之间的重叠。

这些限制源于当前对高斯的解释，阻碍了 3D 语义高斯表示的效率和有效性。我们的方法从概率角度出发，以根本性的方式解决这些问题，如图 2 所示。

3.2 概率高斯叠加

我们提出了概率高斯叠加作为一种高效且有效的 3D 场景表示方法。如图 3 所示，我们将 3D 建模目标分解为几何和语义预测，并分别从概率角度采用概率的乘法定理和高斯混合模型来处理它们。

注

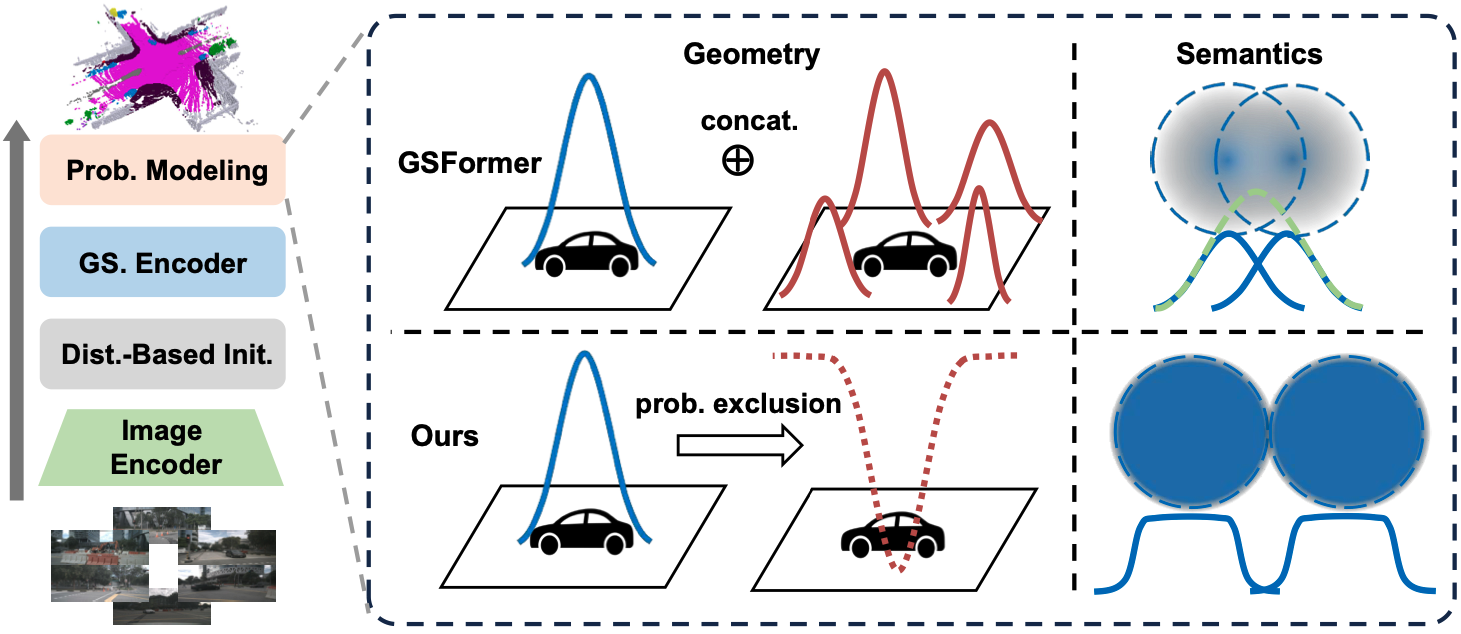
**图 3. 我们方法的整体流程。**为了实现概率建模，我们将占用预测分解为几何预测和语义预测，并分别采用概率乘法和高斯混合模型来处理它们，以提高效率。

几何预测：

为了限制高斯仅对占用区域进行几何预测，我们将高斯基元 $G = \{G_i\}_{i=1}^P$解释为其周围空间被占用的概率。

具体来说，我们在高斯的中心处分配 100% 的概率值，该值随着与中心 $m$的距离呈指数衰减：

$$\alpha(x; G) = \exp\left(-\frac{1}{2}(x - m)^T \Sigma^{-1}(x - m)\right),$$

其中 $\alpha(x; G)$表示由高斯 $G$诱导的点 $x$被占用的概率。

方程 (4) 在点 $x$接近高斯 $G$的中心时分配较高的占用概率，从而防止任何高斯描述空区域。为了进一步推导出整体占用概率，我们假设不同高斯使点被占用的概率是相互独立的，因此我们可以根据概率的乘法定理进行聚合：

$$\alpha(x) = 1 - \prod_{i=1}^{P} \left(1 - \alpha(x; G_i)\right),$$

其中 $\alpha(x)$表示点 $x$处的整体占用概率。除了实现以目标为中心的特性外，方程 (5) 还避免了高斯之间的不必要重叠，因为对于任何高斯 $G_i$，都有 $\alpha(x) \geq \alpha(x; G_i)$。这意味着如果点 $x$足够接近任何一个高斯，它将被预测为被占用。

语义预测：

除了以目标为中心且避免重叠的几何建模外，我们还需要为语义预测实现相同的目标。我们首先从高斯的语义属性 $c$中移除表示空类别的通道，因为这已经在几何预测中被考虑过了。然后我们将高斯集合 $G$解释为高斯混合模型，其中语义预测可以被表述为计算给定概率高斯混合模型的语义期望。

注

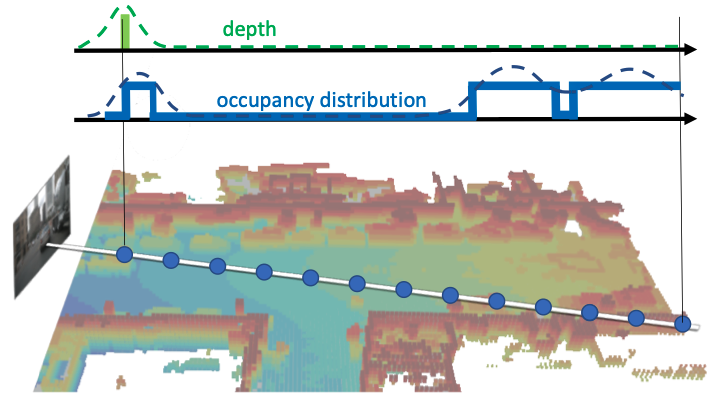
**图 4. 基于分布的初始化。**我们的初始化方案从占用注释中学习像素对齐的占用分布，而基于深度的对应方案仅捕获物体的表面，并依赖于激光雷达监督。

• 具体来说，我们采用原始不透明度属性 $a$作为高斯的先验分布，并对其进行 $l1$ 归一化。

• 此外，我们采用由均值 $m$、尺度 $s$和旋转 $r$参数化的高斯概率分布作为条件概率。

• 然后我们使用 softmax 对原始语义属性 $c$进行归一化，以确保预测语义的有界性。最后，我们计算期望 $e(x; G)$：

$$e(x; G) = \sum_{i=1}^{P} p(G_i|x) \tilde{c}_i = \frac{\sum_{i=1}^{P} p(x|G_i) a_i \tilde{c}_i}{\sum_{j=1}^{P} p(x|G_j) a_j},$$

$$p(x|G_i) = \frac{1}{(2\pi)^{3/2} |\Sigma|^{1/2}} \exp\left(-\frac{1}{2}(x - m)^T \Sigma^{-1}(x - m)\right),$$

其中 $p(G_i|x)$、$p(x|G_i)$和 $\tilde{c}_i$分别表示点 $x$属于第 $i$个高斯分布的后验概率、点 $x$给定第 $i$个高斯分布的条件概率以及经过 softmax 归一化的语义属性。

与方程 (1) 和 (2) 相比，方程 (6) 中的高斯混合模型对语义属性和不同高斯的贡献进行了归一化，从而防止了高斯之间的不必要重叠，并直接产生归一化的类别概率。

鉴于几何和语义预测，我们简单地将它们结合起来生成最终的语义占用预测：

$$\hat{o}(x; G) = [1 - \alpha(x); \alpha(x) \cdot e(x; G)],$$

其中我们使用几何概率 $\alpha(x)$来加权语义预测，并直接将 $1 - \alpha(x)$作为空类别的概率。

3.3 基于分布的初始化

先前的 3D 语义高斯表示采用可学习的初始化策略，该策略在训练开始时随机初始化高斯的属性，并以数据驱动的方式优化这种初始化。这种策略使模型能够学习整个数据集的占用先验分布，这依赖于网络后续的细化以适应每个单独样本的分布。

然而，高斯的局部感受野限制了它们的移动性，这阻碍了每个高斯在后续细化中学习到达正确位置的路径。而且，对于我们的概率高斯叠加来说，这个问题更为严重，因为高斯仅用于建模占用区域。

为了解决这一问题，我们提出了一个基于分布的初始化模块，为高斯提供更准确且整体的样本特定初始化，如图 4 所示。我们用从 2D 主干网络中提取的图像特征监督像素对齐的占用分布，该分布是从占用注释中得出的。

具体来说，我们首先根据相机标定数据确定每条图像特征对应的射线的原点 $b$和方向 $d$。

然后，我们在该射线上等间隔地采样 $R$个参考点，这些点在一个固定的深度范围内。对于这些参考点中的每一个，我们在相应位置查询真实占用 $O$，以获得二进制标签 $l = \{l_i\}_{i=1}^R$，表示参考点是否被占用。然后，我们使用 $l = \{l_i\}_{i=1}^R$作为监督来优化我们的初始化模块，该模块由图像主干网络 $B$和分布预测器 $M$组成。

分布预测器 $M$直接将图像特征解码为沿对应射线的占用分布 $\hat{l}$，并使用二进制交叉熵损失与 $l$进行匹配：

$$\text{loss}_{\text{init}} = \text{BCE}(\hat{l}, l) = \text{BCE}(M(B(I)), l).$$

与先前的初始化方案不同，这些方案在激光雷达监督下预测深度值，我们的方法学习整体的占用分布，而不是仅学习场景的可见表面，并且不需要任何额外的模态作为监督。

总体而言，我们的基于分布的初始化模块初始化了高斯，随后将它们送入 GaussianFormer [15] 中的注意力架构块。每个块包括自编码、图像交叉注意力和细化模块，在这些模块中，概率高斯属性稳步改进，然后通过我们新提出的方法对结果高斯进行聚合，该方法鼓励高斯的更高利用率。

4. 实验

4.1 数据集和评估指标

nuScenes 数据集 [2] 提供了 1000 个场景，涵盖了波士顿和新加坡的环绕视图驾驶场景。官方划分为 700/150/150 个场景，分别用于训练、验证和测试。每个场景持续 20 秒，并以 2Hz 的频率进行全标注，数据来自 5 个雷达、6 个相机、1 个激光雷达和 1 个惯性测量单元（IMU）。我们使用 SurroundOcc [44] 提供的 3D 语义占用注释进行监督和评估。占用注释在 $x$、$y$和 $z$轴上的范围（以米为单位）分别为 $[-50, 50]$、$[-50, 50]$和 $[-5, 3]$，每个体素的边长为 0.5 米，并被标记为 18 个可能类别中的一个（16 个语义类别、1 个空类别和 1 个噪声类别）。KITTI-360 数据集 [26] 包含超过 320k 张郊区图像，配备了丰富的 360 度传感器真值，包括 2 个透视相机、2 个鱼眼相机、1 个 Velodyne 激光雷达和 1 个激光扫描仪，我们使用自车左相机的图像作为模型的输入。对于 3D 语义占用预测，我们采用 SSCBench-KITTI-360 [21] 提供的注释。官方划分是 7/1/1 个序列，分别用于训练、验证和测试，分别有 8487/1812/2566 个关键帧。体素网格区域覆盖了自车前方 $51.2 \times 51.2 \times 6.4 \, \text{m}^2$的范围，分辨率为 $256 \times 256 \times 32$。每个体素被分类为 19 个类别中的一个（18 个语义类别和 1 个空类别）。评估指标遵循常见做法 [3]，即平均交并比（mIoU）和交并比（IoU）：

$$\text{mIoU} = \frac{1}{|C'|} \sum_{i \in C'} \frac{\text{TP}_i}{\text{TP}_i + \text{FP}_i + \text{FN}_i},$$

$$\text{IoU} = \frac{\text{TP}_{c_0}}{\text{TP}_{c_0} + \text{FP}_{c_0} + \text{FN}_{c_0}},$$

其中 $C'$、$c_0$、$\text{TP}$、$\text{FP}$和 $\text{FN}$分别表示非空类别、空类别以及真正例、假正例和假负例的数量。

4.2 实现细节

nuScenes [2] 的输入图像分辨率为 $900 \times 1600$，KITTI-360 [26] 的输入图像分辨率为 $376 \times 1408$，我们对输入图像进行了随机翻转和光度畸变增强。我们使用与 GaussianFormer [15] 相同的图像主干网络检查点，即 nuScenes 使用 ResNet101-DCN [10] 和 FCOS3D 检查点 [43]，KITTI-360 使用在 ImageNet [9] 上预训练的 ResNet50 [10]。我们在 nuScenes 和 KITTI-360 的主要结果中分别将高斯的数量设置为 12800 和 38400。我们使用 AdamW [29] 进行模型训练，权重衰减为 0.01，最大学习率为 $2 \times 10^{-4}$，并采用余弦退火计划进行衰减。我们在 nuScenes 上训练了 20 个 epoch，批次大小为 8，在 KITTI-360 上训练了 30 个 epoch，批次大小为 4。

4.3 主要结果

环绕视图 3D 语义占用预测：我们在表 1 中报告了 GaussianFormer-2 的性能。我们的方法相比其他方法实现了最先进的性能。具体来说，GaussianFormer-2 在自行车和摩托车等类别上超越了基于密集网格表示的方法，证明了我们提出的概率高斯叠加在建模小物体方面的灵活性。此外，我们的方法以显著更少的高斯数量（12800 对 144000）明显优于 GaussianFormer [15]，验证了我们的方法的效率和有效性。

单目 3D 语义占用预测：我们在表 2 中报告了在 SSCBench-KITTI-360 [21] 上的单目 3D 语义占用预测结果。我们的方法实现了最先进的性能，与 GaussianFormer 相比，mIoU 提高了 7.6%。具体来说，我们在道路、人行道和建筑物等类别的 mIoU 上取得了显著提升，这表明概率高斯叠加在建模背景物体方面的优越性。

4.4 消融研究

高斯数量：我们在表 3 中报告了高斯数量对我们的模型效率和性能的影响。我们的模型相比 GaussianFormer 实现了更好的性能与效率权衡，仅使用不到 5% 的高斯数量就超越了它。我们的方法的延迟高于 GaussianFormer，我们认为这是由于我们初始化模块中耗时的最远点采样（FPS）操作。我们采用分而治之的策略，以分批的方式进行 FPS 操作以加速，并在括号中报告初始化模块的延迟。

设计选择：我们在表 4 中对 GaussianFormer-2 的设计选择进行了消融研究。我们观察到，概率建模和基于分布的初始化模块均带来了一致的提升，并且明显优于基于深度的对应方案。

高斯的利用率：我们在表 5 中使用两个重要指标来比较 GaussianFormer [15] 和我们的方法对高斯的利用率，这些指标分别是位置和重叠。高斯处于正确位置的百分比（Perc.）是均值位于占用空间中的高斯数量的百分比。总体重叠是通过计算所有高斯在 90% 覆盖体积中的体积总和得出的，而个体重叠则是通过计算每个高斯与其他所有高斯之间的 Bhattacharyya 系数的平均值得出的。我们在附录中提供了这些指标的详细信息。我们的方法在所有这些指标上均优于 GaussianFormer，证明了更好的利用率。

4.5 可视化

我们在图 5 中提供了高斯和占用的可视化结果。我们的模型能够预测出合理的高斯分布和全面的占用结果。此外，我们在图 6 中将我们的方法与 GaussianFormer [15] 进行了对比。我们的方法预测的 3D 高斯具有更适应性的形状，与 GaussianFormer 中的各向同性球形高斯相比更具优势。尽管我们的方法仅使用了 8.8% 的高斯数量，但仍然能够生成全面的占用预测，并缓解了 GaussianFormer 中的拉伸效应。

我们在图 7 中可视化了 GaussianFormer-2 在初始化和后续块中的高斯的 $xy$坐标。我们发现，由于以目标为中心的概率设计和有效的初始化模块，高斯成功地学习了向占用区域移动。

5. 结论

在本文中，我们提出了一个概率高斯叠加模型，作为一种高效的以目标为中心的表示方法。具体来说，我们将每个高斯解释为其邻域被占用的概率分布，并采用概率的乘法定理来推导几何预测。我们还采用高斯混合模型公式来计算归一化的语义预测。我们还设计了一个基于分布的初始化策略，以有效地在占用区域周围初始化高斯，以实现根据像素对齐的占用分布进行以目标为中心的建模。我们的 GaussianFormer-2 在 nuScenes 和 KITTI-360 数据集上针对 3D 语义占用预测实现了最先进的性能，并且相比 GaussianFormer，在高斯数量、位置正确性和重叠比率方面也展现了更高的效率。

补充材料

A. 视频演示

图 8 展示了我们在 nuScenes 数据集 [2] 上进行 3D 语义占用预测的视频演示的一个样本帧。我们注意到，相机视角的占用可视化与输入 RGB 图像非常吻合。此外，每个实例仅通过少量具有自适应形状的高斯来稀疏描述，这展示了我们模型的效率和以目标为中心的特性。

B. KITTI-360 上的可视化

我们在图 9 中提供了 KITTI-360 数据集 [26] 上的高斯和占用的可视化结果。我们观察到，我们的 GaussianFormer-2 能够预测出 3D 场景的复杂几何形状和语义信息。此外，我们模型中的 3D 高斯根据它们所描述的具体物体具有自适应的尺度，与 GaussianFormer [15] 中具有最大尺度的各向同性球形高斯相比，这一点尤为明显。

C. 评估指标细节

位置：即使经过完整训练，高斯仍可能被发现在未占用空间中，这是由于其局部感受野的特性。这些高斯未能描述有意义的结构，因此它们是无效的，并且缺乏实际用途。在未占用空间中发现的高斯比例越高，表明模型容量的利用效率越低。因此，我们定义高斯处于正确位置的百分比（Perc.）为：

$$\text{Perc.} = \frac{N_{\text{correct}}}{N_{\text{total}}} \times 100\%,$$

其中 $N_{\text{correct}}$和 $N_{\text{total}}$分别表示均值位于占用空间中的高斯数量和高斯的总数。较高的百分比表明高斯与空间中的占用或有意义区域更好地对齐，从而反映了模型容量的更高效利用。上述测量方法提供了一种硬性评估，其中高斯被二元地分类为处于正确或错误的位置，而没有考虑它们与最近占用区域的接近程度。这种二元方法未能捕捉到未占用区域中高斯与有意义位置的接近程度。为了解决这一局限性，我们定义了一个互补的软性测量方法，即每个高斯与其最近占用体素中心之间的平均距离，用 $\text{Dist.} $（以米为单位）表示，计算如下：

$$\text{Dist.} = \frac{1}{P} \sum_{i=1}^{P} \min_{v \in V} \|m_i - v\|_1,$$

其中 $m_i$、$V$、$v$和 $\|m_i - v\|_1$分别表示第 $i$个高斯的均值、占用体素中心的集合、该集合中的一个体素中心以及高斯均值与体素中心之间的 $L1$距离。请注意，此距离是相对于体素中心计算的，因此位于正确占用区域内的高斯也可能具有非零距离。

重叠：高斯的总体重叠比率（Overall.）从全局角度提供了高斯表示中冗余程度的视角。每个高斯被建模为一个椭球体，其半轴长度是从对应于高斯分布的 90% 置信水平的卡方值 $\chi^2_{3,0.9} \approx 6.251 $的马氏距离导出的。然后，Overall. 被计算为所有高斯的 90% 置信体积 $V_{i,90%} $之和与场景中所有高斯的总覆盖体积 $V_{\text{coverage}} $的比率：

$$\text{Overall.} = \frac{\sum_{i=1}^{P} V_{i,90\%}}{V_{\text{coverage}}},$$

其中 $V_{\text{coverage}} $表示将所有高斯组合成一个统一形状的体积。为了估计 $V_{\text{coverage}} $，我们采用蒙特卡洛方法，在场景的边界框内随机采样大量点。对于每个采样点，我们检查它是否位于至少一个高斯的 90% 置信椭球体内。然后，体积被近似为：

$$V_{\text{coverage}} = V_{\text{scene}} \times \frac{N_{\text{in}}}{N_{\text{total}}},$$

其中 $N_{\text{in}} $和 $N_{\text{total}} $分别是落在至少一个高斯的 90% 置信椭球体内的采样点数量和总采样点数量。这种方法确保了对统一体积的准确估计，有效地处理了高斯之间的重叠区域，避免了重复计数。接下来，我们详细阐述对应于 3D 高斯分布的 90% 置信区域的椭球体体积的推导。

考虑一个 3D 多元高斯分布，其定义为：

$$g(x) = \frac{1}{(2\pi)^{3/2} |\Sigma|^{1/2}} \exp\left(-\frac{1}{2}(x - m)^T \Sigma^{-1}(x - m)\right),$$

其中 $x $、$\Sigma $和 $|\Sigma| $分别是均值向量、3x3 协方差矩阵和协方差矩阵的行列式。点 $x $从均值 $m $的马氏距离 $d $定义为：

$$d^2(x, m) = (x - m)^T \Sigma^{-1}(x - m).$$

高斯分布的 90% 置信区域对应于满足以下条件的点集，马氏距离满足：

$$d^2 \leq \chi^2_{3,0.9} \approx 6.251,$$

其中 $\chi^2_{3,0.9} $是在 90% 置信水平下，3 个自由度的卡方临界值。对于高斯分布，半轴长度由 $\Sigma $的特征值的平方根决定，按 $\chi^2_{3,0.9} $缩放。因此，对应于 3D 高斯分布 90% 的椭球体体积为：

$$V_{90\%} = \frac{4}{3} \pi (6.251)^{3/2} |\Sigma|^{1/2}.$$

较高的 Overall. 值表明高斯之间的重叠体积更大，表明高斯表示存在冗余。这一指标提供了关于高斯用于表示场景的利用情况的见解。高斯之间的个体重叠比率（Indiv.）提供了对场景中高斯之间重叠程度的细粒度分析。这一指标量化了每个高斯与其他所有高斯之间的重叠程度，并取场景中所有高斯的平均值。该指标的值大致表示单个高斯的体积平均与其他高斯完全重叠的次数。为了计算这一指标，我们使用 Bhattacharyya 系数 [1]，它衡量两个高斯分布之间的相似性。个体重叠比率定义为：

$$\text{Indiv.} = \frac{1}{P} \sum_{i=1}^{P} \left( \sum_{j \neq i} \text{BC}_{i,j} \right),$$

其中 $\text{BC}_{i,j} $是第 $i $个和第 $j $个高斯之间的 Bhattacharyya 系数，由下式给出：

$$\text{BC}_{i,j} = \sqrt{\frac{|\Sigma_i| |\Sigma_j|}{|\Sigma_{ij}|}} \exp\left(-\frac{1}{8}(m_i - m_j)^T \Sigma_{ij}^{-1}(m_i - m_j)\right),$$

其中 $\Sigma_{ij} = \frac{1}{2}(\Sigma_i + \Sigma_j) $是平均协方差矩阵。较高的 Indiv. 值表明存在更多的冗余，因为高斯之间存在大量重叠。